Регрессионный анализ в эксель пример. Математические методы в психологии
Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.
Основные задачи и виды регрессии
Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.
Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.
Основные задачи построения регрессионной модели заключаются в следующем:
- Отбор значимых независимых переменных (Х1, Х2, …, Xk).
- Выбор вида функции.
- Построение оценок для коэффициентов.
- Построение доверительных интервалов и функции регрессии.
- Проверка значимости вычисленных оценок и построенного уравнения регрессии.
Регрессионный анализ бывает нескольких видов:
- парный (1 зависимая и 1 независимая переменные);
- множественный (несколько независимых переменных).
Уравнения регрессии бывает двух видов:
- Линейные, иллюстрирующие строгую линейную связь между переменными.
- Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.
Инструкция построения модели
Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.
В Excel имеется еще более быстрый и удобный способ построить график линейной регрессии (и даже основных видов нелинейных регрессий, о чем см. далее). Это можно сделать следующим образом:
1) выделить столбцы с данными X и Y (они должны располагаться именно в таком порядке!);
2) вызвать Мастер диаграмм и выбрать в группе Тип – Точечная и сразу нажать Готово ;
3) не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма , в котором следует выбрать пункт Добавить линию тренда ;
4) в появившемся диалоговом окне Линия тренда во вкладке Тип выбрать Линейная ;
5) во вкладке Параметры можно активизировать переключатель Показывать уравнение на диаграмме , что позволит увидеть уравнение линейной регрессии (4.4), в котором будут вычислены коэффициенты (4.5).
6) В этой же вкладке можно активизировать переключатель Поместить на диаграмму величину достоверности аппроксимации (R^2) . Эта величина есть квадрат коэффициента корреляции (4.3) и она показывает, насколько хорошо рассчитанное уравнение описывает экспериментальную зависимость. Если R 2 близок к единице, то теоретическое уравнение регрессии хорошо описывает экспериментальную зависимость (теория хорошо согласуется с экспериментом), а если R 2 близок к нулю, то данное уравнение не пригодно для описания экспериментальной зависимости (теория не согласуется с экспериментом).
В результате выполнения описанных действий получится диаграмма с графиком регрессии и ее уравнением.
§4.3. Основные виды нелинейной регрессии
Параболическая и полиномиальная регрессии.
Параболической зависимостью величины Y от величины Х называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):
Это уравнение называется уравнением параболической регрессии Y на Х . Параметры а , b , с называются коэффициентами параболической регрессии . Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.
Уравнение (4.8) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной зависимостью величины Y от величины Х называется зависимость, выраженная полиномом n -ого порядка:
где числа а i (i =0,1,…, n ) называются коэффициентами полиномиальной регрессии .
Степенная регрессия.
Степенной зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением степенной регрессии Y на Х . Параметры а и b называются коэффициентами степенной регрессии .
ln =lna +b· lnx . (4.11)
Это уравнение описывает прямую на плоскости с логарифмическими координатными осями lnx и ln . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки логарифмов эмпирических данных lnx i и lnу i находились ближе всего к прямой (4.11).
Показательная регрессия.
Показательной (или экспоненциальной ) зависимостью величины Y от величины Х называется зависимость вида:
(или ). (4.12)
Это уравнение называется уравнением показательной (или экспоненциальной ) регрессии Y на Х . Параметры а (или k ) и b называются коэффициентами показательной (или экспоненциальной ) регрессии .
Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение
ln =x· lna +lnb (или ln =k·x +lnb ). (4.13)
Это уравнение описывает линейную зависимость логарифма одной величины ln от другой величины x . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки эмпирических данных одной величины x i и логарифмы другой величины lnу i находились ближе всего к прямой (4.13).
Логарифмическая регрессия.
Логарифмической зависимостью величины Y от величины Х называется зависимость вида:
=a +b· lnx . (4.14)
Это уравнение называется уравнением логарифмической регрессии Y на Х . Параметры а и b называются коэффициентами логарифмической регрессии .
Гиперболическая регрессия.
Гиперболической зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением гиперболической регрессии Y на Х . Параметры а и b называются коэффициентами гиперболической регрессии и определяются методом наименьших квадратов. Применение этого метода приводит к формулам:
В формулах (4.16-4.17) суммирование проводится по индексу i от единицы до количества наблюдений n .
К сожалению, в Excel нет функции, вычисляющих коэффициенты гиперболической регрессии. В тех случаях, когда заведомо не известно, что измеряемые величины связаны обратной пропорциональностью, рекомендуется вместо уравнения гиперболической регрессии искать уравнение степенной регрессии, так в Excel имеется процедура ее нахождения. Если же между измеряемыми величинами предполагается гиперболическая зависимость, то коэффициенты ее регрессии придется вычислять с помощью вспомогательных расчетных таблиц и операций суммирования по формулам (4.16-4.17).
Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
ŷ — ожидаемое значение у при заданном значении х,
x — независимая переменная,
a — отрезок на оси y для прямой линии,
b — наклон прямой линии.
На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х = 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг - определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по .
Использование Excel для определения линейной регрессии
Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа . Найти ее можно, перейдя по вкладке Файл –> Параметры (2007+), в появившемся диалоговом окне Параметры Excel переходим во вкладку Надстройки. В поле Управление выбираем Надстройки Excel и щелкаем Перейти. В появившемся окне ставим галочку напротив Пакет анализа, жмем ОК.

Во вкладке Данные в группе Анализ появится новая кнопка Анализ данных.

Чтобы продемонстрировать работу надстройки, воспользуемся данными , где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.
Перейдите во вкладку Данные, в группе Анализ щелкните Анализ данных. В появившемся окне Анализ данных выберите Регрессия , как показано на рисунке, и щелкните ОК.

Установите необходимыe параметры регрессии в окне Регрессия , как показано на рисунке:

Щелкните ОК. На рисунке ниже показаны полученные результаты:
Эти результаты соответствуют тем, которые мы получили путем самостоятельных вычислений в .
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k объясняющих переменных) по данным примера 3.6.
В таблице регрессионной статистики приводятся значения:
Множественный R – коэффициент множественной корреляции ;
R - квадрат – коэффициент детерминации R 2 ;
Нормированный R - квадрат – скорректированный R 2 с поправкой на число степеней свободы;
Стандартная ошибка – стандартная ошибка регрессии S ;
Наблюдения – число наблюдений n .
В таблице Дисперсионный анализ приведены:
1. Столбец df - число степеней свободы, равное
для строки Регрессия df = k ;
для строкиОстаток df = n – k – 1;
для строкиИтого df = n – 1.
2. Столбец SS – сумма квадратов отклонений, равная
для строки Регрессия ;
для строкиОстаток ;
для строкиИтого .
3. Столбец MS дисперсии, определяемые по формуле MS = SS /df :
для строки Регрессия – факторная дисперсия;
для строкиОстаток – остаточная дисперсия.
4. Столбец F – расчетное значение F -критерия, вычисляемое по формуле
F = MS (регрессия)/MS (остаток).
5. Столбец Значимость F –значение уровня значимости, соответствующее вычисленной F -статистике.
Значимость F = FРАСП(F- статистика, df (регрессия), df (остаток)).
Если значимость F < стандартного уровня значимости, то R 2 статистически значим.
| Коэффи-циенты | Стандартная ошибка | t-cта-тистика | P-значение | Нижние 95% | Верхние 95% | |
| Y | 65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X | 0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты – значения коэффициентов a , b .
2. Стандартная ошибка –стандартные ошибки коэффициентов регрессии S a , S b .
3. t- статистика – расчетные значения t -критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р -значение (значимость t ) – это значение уровня значимости, соответствующее вычисленной t- статистике.
Р -значение = СТЬЮДРАСП (t -статистика, df (остаток)).
Если Р -значение < стандартного уровня значимости, то соответствующий коэффициент статистически значим.
5. Нижние 95% и Верхние 95% – нижние и верхние границы 95 %-ных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии.
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное y | Остатки e |
| 72,70 | -29,70 | |
| 82,91 | -20,91 | |
| 94,53 | -4,53 | |
| 105,72 | 5,27 | |
| 117,56 | 12,44 | |
| 129,70 | 19,29 | |
| 144,22 | 20,77 | |
| 166,49 | 24,50 | |
| 268,13 | -27,13 |
В таблице ВЫВОД ОСТАТКА указаны:
в столбце Наблюдение – номер наблюдения;
в столбце Предсказанное y – расчетные значения зависимой переменной;
в столбце Остатки e – разница между наблюдаемыми и расчетными значениями зависимой переменной.
Пример 3.6. Имеются данные (усл. ед.) о расходах на питание y и душевого дохода x для девяти групп семей:
| x | |||||||||
| y |
Используя результаты работы пакета анализа Excel (Регрессия), проанализируем зависимость расходов на питание от величины душевого дохода.
Результаты регрессионного анализа принято записывать в виде:
![]()
где в скобках указаны стандартные ошибки коэффициентов регрессии.
Коэффициенты регрессии а = 65,92 и b = 0,107. Направление связи между y и x определяет знак коэффициентарегрессии b = 0,107, т.е. связь является прямой и положительной. Коэффициент b = 0,107 показывает, что при увеличении душевого дохода на 1 усл. ед. расходы на питание увеличиваются на 0,107 усл. ед.
Оценим значимость коэффициентов полученной модели. Значимость коэффициентов (a, b ) проверяется по t -тесту:
Р-значение (a ) = 0,00080 < 0,01 < 0,05
Р-значение (b ) = 0,00016 < 0,01 < 0,05,
следовательно, коэффициенты (a, b ) значимы при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости. Таким образом, коэффициенты регрессии значимы и модель адекватна исходным данным.
Результаты оценивания регрессии совместимы не только с полученными значениями коэффициентов регрессии, но и с некоторым их множеством (доверительным интервалом). С вероятностью 95 % доверительные интервалы для коэффициентов есть (38,16 – 93,68) для a и (0,0728 – 0,142) для b.
Качество модели оценивается коэффициентом детерминации R 2 .
Величина R 2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R 2 проверяется по F- тесту: значимость F = 0,00016 < 0,01 < 0,05, следовательно, R 2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как ![]() . Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
. Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН
.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
4) В окне Категория
выберете Статистические
, в окне функция - ЛИНЕЙН
. Щёлкните по кнопке ОК
как показано на Рисунке 2;

Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у
Известные значения х
Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК ;

Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Стандартная ошибка y | |
| F-статистика | |
| Регрессионная сумма квадратов
|

Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х - среднедушевого прожиточного минимума, а 48% - действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: ![]() .
.
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.

Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия
можно получить:
- результаты регрессионной статистики,
- результаты дисперсионного анализа,
- результаты доверительных интервалов,
- остатки и графики подбора линии регрессии,
- остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y - диапазон, содержащий данные результативного признака;
Входной интервал X - диапазон, содержащий данные факторного признака;
Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа - ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист - можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

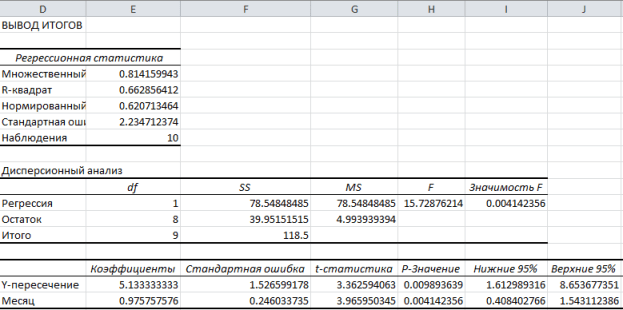
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
![]()

Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 - 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: ![]()
Поскольку ![]() при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
![]() .
.
![]() для числа степеней свободы
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где  - случайная ошибка коэффициента корреляции.
- случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.

II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
![]()
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
![]()
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
![]()
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью ![]() параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:

где ![]()
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .

Рисунок 10 Расчёт дисперсии
Получили значение дисперсии ![]()
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
![]()
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2003. - 192 с.: ил.